Question

Quick help! Exponential modelling

The temperature (T) of a dish t minutes after it is removed from the microwave, is given by:


`T(t) = 55 * ({0.913})^(t) +22°C`

a) What is the initial temperature of the dish?

b) What is the temperature after,
(i) 12 minutes

(ii) 36 minutes​

Answer 1

a) 77 degrees Celsius

bi) 40.45066 degrees Celsius

bii) 24.0764 degree Celsius

Explanation:

I'm assuming the temperature function is:

`T(t)=55(0.913)^t+22`.

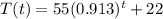a) The initial temperature can be found by replacing t with 0.

`T(0)=55(0.913)^0+22`

`T(0)=55(1)+22`

`T(0)=55+22`

`T(0)=77`

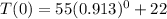
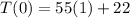
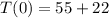
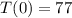
bi) We are to replace t with 12:

`T(12)=55(0.913)^(12)+22`

Just put right hand side into the calculator as:

55*(0.913)^12+22 which should output 40.45066 approximately.

bii) We are to replace t with 36:

`T(36)=55(0.913)^(36)+22`

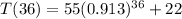
Putting right hand side into calculator as 55*(0.913)^36+22 gives:

24.0764 approximately.