Answer:
Part 4) Yes, the relationship between cups of milk and cups of cereal can be described by a constant ratio, and this ratio is equal to 1/3
Part 5) Yes, the relationship between cups of cereal and servings of cereal can be described by a constant ratio, and this ratio is equal to 3/4
Explanation:
Part 4) Can the relationship between cups of milk and cups of cereal be described by a constant ratio?
Let
x ------> cups of milk
y -----> cups of cereal
observing the table
For x=4, y=12
so
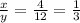
For x=6, y=18
so
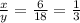
The relationship between cups of milk and cups of cereal is proportional
therefore
Yes, can be described by a constant ratio, and this ratio is equal to 1/3
Part 5) Can the relationship between cups of cereal and servings of cereal be described by a constant ratio?
Let
x ------> cups of cereal
y -----> servings of cereal
observing the table
For x=12, y=16
so
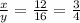
For x=18, y=24
so
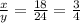
The relationship between cups of cereal and servings of cereal is proportional
therefore
Yes, can be described by a constant ratio, and this ratio is equal to 3/4