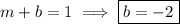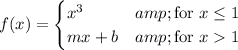
 must be continuous in order to be differentiable, so we need to have
must be continuous in order to be differentiable, so we need to have

By its definition,
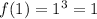 , and
, and
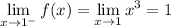
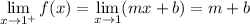
so that
 .
.
We want the derivative to exist at
 , which requires that we pick an appropriate value for
, which requires that we pick an appropriate value for
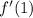 so that
so that
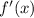 is also continuous. At the moment, we know
is also continuous. At the moment, we know
![f'(x)=\begin{cases}3x^2&\text{for }x<1\\m&\text{for }x>1\end{cases}{/tex]</p><p>so we need to pick [tex]f'(1)](https://img.qammunity.org/2020/formulas/mathematics/high-school/tflggqfoel9wd48fhlnmwca0n3mumb69ag.png) such that
such that
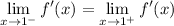
We have
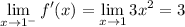
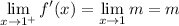
so that
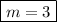 (which means we need to pick
(which means we need to pick
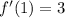 ) and so
) and so