Question

A thin string 2.50 m in length is stretched with a tension of 90.0 N between two supports. When the string vibrates in its first overtone, a point at an antinode of the standing wave on the string has an amplitude of 3.50 cm and a maximum transverse speed of 28.0 m/s. (a) What is the string’s mass? (b) What is the magnitude of the maximum transverse acceleration of this point on the string?

Answer 1

The string's mass and the maximum transverse acceleration are 2.2 g and 22400.51 m/s².

Step-by-step explanation:

Given that,

Length of string = 2.50 m

Tension = 90.0 N

Amplitude = 3.50 cm

Speed = 28.0

First overtone ,

`\lambda =l`

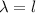
(a). We need to calculate the mass of string

Using maximum transverse speed at antinodes

`v_(max)=A\omega`

`A\omega=28`

`A*2\pi f=28`

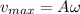
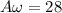
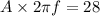
Put the value into the formula

`f=(28)/(2*3.14*3.50*10^(-2))`

`f=127.39\ Hz`

Using formula of wavelength

`v = f\lambda`

`\sqrt{(T)/(\mu)}=f\lambda`

`\mu=(90)/((127.39*2.50)^2)`

`\mu=8.8734*10^(-4)`

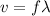
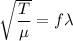
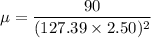
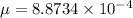
Mass of string =
`\mu* l`

Mass of string =
`8.8*10^(-4)*2.50`

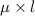
Mass of string =2.2 g

(b). We need to calculate the maximum transverse acceleration of this point on the string

Using formula of the maximum transverse acceleration

`a=A\omega^2`

`a=A*(2\pif)^2`

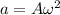
Put the value into the formula

`a=3.50*10^(-2)(*2*3.14*127.39)^2`

`a=22400.51\ m/s^2`

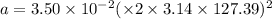
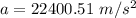
Hence, The string's mass and the maximum transverse acceleration are 2.2 g and 22400.51 m/s².