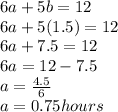Question

Keisha the trainer has two solo workout plans that she offers her clients: Plan A and Plan B. Each client does either one or the other (not both). On Wednesday there were 2 clients who did Plan A and 3 who did Plan B. On Thursday there were 6 clients who did Plan A and 5 who did Plan B. Keisha trained her Wednesday clients for a total of 6 hours and her Thursday clients for a total of 12 hours. How long does each of the workout plans last?

Answer 1

Plan A last 0.75 hours or 45 minutes.

Plan B last 1.5 hours or 90 minutes.

Explanation:

Let
`a` be the number of hours that the plan A last, an
`b` the number of hours of plan B. Then for the Wednesday you have:

`2a+3b=6`

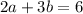
And for the Thursday is:

`6a+5b=12`

Multiply the equation of Wednesday by -3:

`-6a-9b=-18`

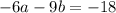
Using the method of addition using this last equation and the equation of Thursday

`-6a-9b=-18\\6a+5b=12\\--------\\-4b=-6\\b=(-6)/(-4)\\b=1.5 hours`

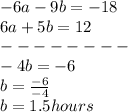
Replacing the value of
`b` in one of the equations

`6a+5b=12\\6a+5(1.5)=12\\6a+7.5=12\\6a=12-7.5\\a=(4.5)/(6) \\a=0.75hours`