Question

Requirements for the width of a tractor engine component are 23.23 +/- 0.612 millimeters. The current process produces components with an average width of 23.546 and a population standard deviation of 0.092. The process is normally distributed. If the control limits are set at +/- 2 standard deviations instead of +/- 3 standard deviations from the mean, what is the Cpk of this process?

Answer 1

The Cpk for the process is 1.61

Explanation:

The formula for Cpk is:

`Cpk=min((USL-mean)/(2*stdDev),(mean-LSL)/(2*stdDev) )`

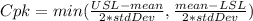
In this case in specific that we can test the capability of the process for 2 standard dev we modify the formula to adjust it:

so for this formula:

average: 23.546

USL: 23.23+0.612=23.842

LSL: 23.23-0.612=22.618

standard dev=0.092

So,

`Cpk=min((23.842-23.546)/(2*0.092) , (23.546-22.618)/(2*0.092) )\\[tex]Cpk=min(1.61 ,5.04 )\\\\Cpk=1.61`\\\\[/tex]

The Cpk for the process is 1.61, so is a good indicator even with the control of two standard dev.