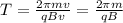Answer:
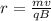 ,
,
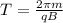
Step-by-step explanation:
The force experienced by the ion due to the magnetic field is given by:

where
q is the charge
v is the speed
B is the intensity of the magnetic field
The cetripetal force is
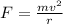
where
m is the mass
r is the radius of the circle
Since the magnetic force acts as centripetal force, we can equate the two expressions:
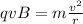
Re-arranging it, we find the radius:
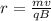
Now, if we want to find the time it takes for the ion to make one complete circle (=the period), we just need to divide the length of one circumference by the speed:
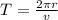
And susbstituting the expression we found before for r, we find