Answer: Our required probability is 0.83.
Explanation:
Since we have given that
Number of dices = 2
Number of fair dice = 1
Probability of getting a fair dice P(E₁) =

Number of unfair dice = 1
Probability of getting a unfair dice P(E₂) =

Probability of getting a 3 for the fair dice P(A|E₁)=

Probability of getting a 3 for the unfair dice P(A|E₂) =

So, we need to find the probability that the die he rolled is fair given that the outcome is 3.
So, we will use "Bayes theorem":
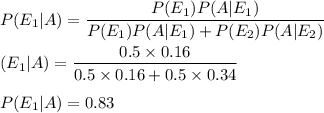
Hence, our required probability is 0.83.