Solve for x in the interval [0,2π]: log₂cot(x) - 2log₄csc(2x) = log₂cos(x)

Question

asked Aug 9, 2020 54.0k views

1 Answer

Dgamboa · Answer 1 · 2020-08-16T16:35:10+0000

Answer:

$x=(\pi)/(3)$

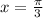
Explanation:

The given logarithmic equation is
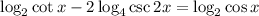$\log_2\cot x-2\log_4\csc 2x=\log_2\cos x$ .

We regroup to get:

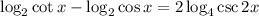$\log_2\cot x-\log_2\cos x=2\log_4\csc 2x$ .

Apply the quotient property of logarithms on the LHS.

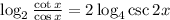$\log_2{(\cot x)/(\cos x)=2\log_4\csc 2x$ .

Apply the power rule and change of base on the RHS

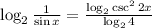$\log_2{(1)/(\sin x)=(\log_2\csc^2 2x)/(\log_24)$ .

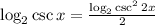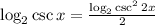$\log_2 \csc x=(\log_2\csc^2 2x)/(2)$ .

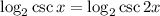$\log_2 \csc x=\log_2\csc 2x$ .

We equate the arguments to get:

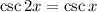
$\csc 2x=\csc x$

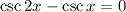
$\csc 2x-\csc x=0$

Or

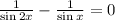
$(1)/(\sin 2x)-(1)/(\sin x)=0$

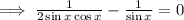
$\implies (1)/(2\sin x\cos x)-(1)/(\sin x)=0$

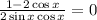
$(1-2\cos x)/(2\sin x \cos x)=0$

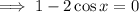
$\implies 1-2\cos x=0$

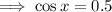
$\implies \cos x=0.5$

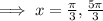
$\implies x=(\pi)/(3),(5\pi)/(3)$

But
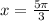$x=(5\pi)/(3)$ is an extraneous solution.

Therefore
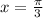$x=(\pi)/(3)$ is the only solution in the interval [0,2π]