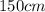Answer:
The perimeter of the larger square is

Explanation:
First of all, let one part of it be "
 "
"
and the other part of it "
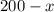 "
"
Now to solve this :
The area of the square =
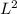
The area of one part of the square =

The area of the other part of the square =

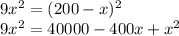
Now, add,
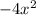 to both the sides :
to both the sides :
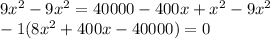
Now, take out the "8" which is common :
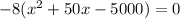
Now, divide it by
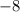 :
:
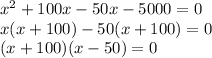
 or
or
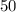
So, now we know that :
One of the part is =
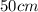
And the other part is =
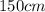
Thus the perimeter of the larger square is =