Question

A gas expands at a constant pressure of 3 atm from a volume of 0.02 cubic meters to 0.10 cubic meters. In the process it experiences an increase in internal energy of 3.0 × 105 joules. (Note: 1 Pa = 1N/m2 and 1 atm = 1.013 × 105 Pa ) What is the work done by the gas? How much heat is absorbed by the gas? Identify the thermodynamic process.

Answer 1

Given: P = 3 atm, Vi = 0.02 m3, Vi = 0.10 m3, ∆U = 3.0 × 105 J

Find: work, W; Heat, Q

W = P(Vf - Vi)

= (3.039 × 105 Pa)(0.08 m3)

= 2.4 × 104 J

Q = ∆U + W

= 3.0 × 105 J + 2 × 104 J

= 3.0 × 105 J

Process: isobaric

Explaination: edmentum

Answer 2

a)
`2.4\cdot 10^4 J`

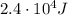
For a gas transformation occuring at a constant pressure, the work done by the gas is given by

`W=p(V_f -V_i)`

where

p is the gas pressure

V_f is the final volume of the gas

V_i is the initial volume

For the gas in the problem,

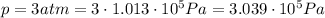`p=3 atm = 3\cdot 1.013\cdot 10^5 Pa = 3.039\cdot 10^5 Pa` is the pressure

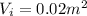`V_i = 0.02 m^2` is the initial volume

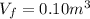`V_f = 0.10 m^3` is the final volume

Substituting,

`W=(3.039\cdot 10^5 Pa)(0.10 m^3-0.02m^2)=24312 J = 2.4\cdot 10^4 J`

b)
`3.24\cdot 10^5 J`

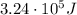
The heat absorbed by the gas can be found by using the 1st law of thermodynamics:

`\Delta U = Q-W`

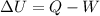
where

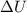`\Delta U` is the change in internal energy of the gas

Q is the heat absorbed

W is the work done

Here we have

`\Delta U = 3.0\cdot 10^5 J`

`W=2.4\cdot 10^4 J`

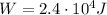
So we can solve the equation to find Q:

`Q=\Delta U + W = 3.0\cdot 10^5 J +2.4\cdot 10^4 J = 3.24\cdot 10^5 J`

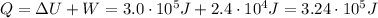
And this process is an isobaric process (=at constant pressure).