The question is incomplete. The complete question is :
The hydrofoil boat has an A-36 steel propeller shaft that is 100 ft long. It is connected to an in-line diesel engine that delivers a maximum power of 2590 hp and causes the shaft to rotate at 1700 rpm . If the outer diameter of the shaft is 8 in. and the wall thickness is
 in.
in.
A) Determine the maximum shear stress developed in the shaft.
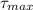 = ?
= ?
B) Also, what is the "wind up," or angle of twist in the shaft at full power?
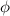 = ?
= ?
Solution :
Given :
Angular speed, ω = 1700 rpm

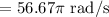
Power
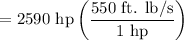
= 1424500 ft. lb/s
Torque,

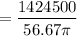
= 8001.27 lb.ft
A). Therefore, maximum shear stress is given by :
Applying the torsion formula
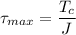
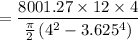
= 2.93 ksi
B). Angle of twist :
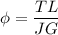
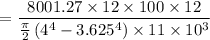
= 0.08002 rad
= 4.58°