Question

The hydrofoil boat has an A-36 steel propeller shaft that is 100 ft long. It is connected to an in-line diesel engine that delivers a maximum power of 2490 hp and causes the shaft to

Answer 1

The question is incomplete. The complete question is :

The hydrofoil boat has an A-36 steel propeller shaft that is 100 ft long. It is connected to an in-line diesel engine that delivers a maximum power of 2590 hp and causes the shaft to rotate at 1700 rpm . If the outer diameter of the shaft is 8 in. and the wall thickness is
`$(3)/(8)$` in.

A) Determine the maximum shear stress developed in the shaft.

`$\tau_(max)$` = ?

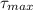B) Also, what is the "wind up," or angle of twist in the shaft at full power?

`$ \phi $` = ?

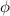Solution :

Given :

Angular speed, ω = 1700 rpm

`$ = 1700 \frac{\text{rev}}{\text{min}}\left(\frac{2 \pi \text{ rad}}{\text{rev}}\right) \frac{1 \text{ min}}{60 \ \text{s}}$`

`$= 56.67 \pi \text{ rad/s}$`

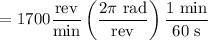
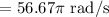
Power
`$= 2590 \text{ hp} \left( \frac{550 \text{ ft. lb/s}}{1 \text{ hp}}\right)$`

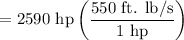
= 1424500 ft. lb/s

Torque,
`$T = (P)/(\omega)$`

`$=(1424500)/(56.67 \pi)$`

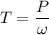
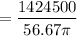
= 8001.27 lb.ft

A). Therefore, maximum shear stress is given by :

Applying the torsion formula

`$\tau_(max) = (T_c)/(J)$`

`$=(8001.27 * 12 * 4)/((\pi)/(2)\left(4^2 - 3.625^4 \right))$`

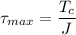
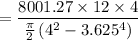
= 2.93 ksi

B). Angle of twist :

`$\phi = (TL)/(JG)$`

`$=(8001.27 * 12 * 100 * 12)/((\pi)/(2)\left(4^4 - 3.625^4\right) * 11 * 10^3)$`

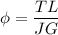
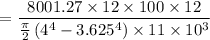
= 0.08002 rad

= 4.58°