Question

The test statistic of zequalsnegative 1.54 is obtained when testing the claim that pless than0.18. a. Using a significance level of alphaequals0.05​, find the critical​ value(s). b. Should we reject Upper H 0 or should we fail to reject Upper H 0​?

Answer 1

(a) The z-critical value for a left-tailed test, for a significance level of α=0.05 is -1.64.

(b) Since -1.54 > -1.64, therefore we accept H₀.

Explanation:

(a)

It is given that the value of test statistic is

`z=-1.54`

We need to test the claim that p<0.18.

Null hypothesis:
`H_0:p=0.18`

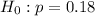
Alternative hypothesis:
`H_1:p<0.18`

It is a left tailed test.

Significance level:

`\alpha=0.05`

The z-critical value for a left-tailed test, for a significance level of α=0.05 is -1.64.

(b)

It is a left tailed test and critical value is -1.64 it means the region on left of -1.64 is rejection region.

The value of z is -1.54 and the critical value is -1.64.

We know that -1.54 > -1.64.

Therefore we accept H₀.