Step-by-step explanation:
It is given that,
Mechanical energy of the block- spring system, E = 3.27 J
Amplitude of the system, A = 10.3 cm = 0.103 m
Maximum speed, v = 1.1 m/s
(a) Mechanical energy of the block spring system is given by :
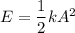
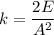
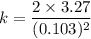
k = 616.45 N/m
(b) Velocity is maximum at the equilibrium position. The mechanical energy at the equilibrium position is given by :
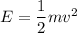
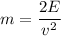
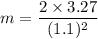
m = 5.4 kg
(c) The frequency of oscillation is :
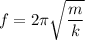

f = 0.58 Hz
Hence, this is the required solution.