Answer:
103.3 %
Step-by-step explanation:
For a radioactive isotope, the number of radioactive nuclei left (parent nuclei) after a time t, N(t), is
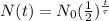
where
N0 is the initial number of radioactive nuclei
t is the time
 is the half-life of the isotope
is the half-life of the isotope
Here we have
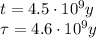
So we find

Which means that the fraction of parent nuclei left after this time is 0.508 (50.8% of the initial value). So the fraction of daugther nuclei at this time is
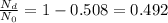
So the percentage of parent to daughter isotopes is
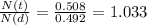
Which corresponds to 103.3 %.