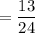Answer with explanation:
Given : The interval for a uniform distribution : (4, 28)
The density function for the uniform distribution will be :-
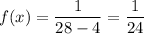
(a) Required interval : (11,24) =
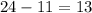
Now, the probability that x lies between 11 and 24 is given by :-
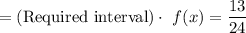
(b) Required interval : (9,22) =
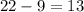
Now, the probability that x lies between 9 and 22 is given by :-
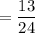
(c) Required interval : (7,19) =
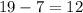
Now, the probability that x lies between 9 and 22 is given by :-
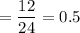
(d)Required interval : (10,23) =
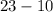
Now, the probability that x lies between 9 and 22 is given by :-