Question

A company has determined that when x hundred dulcimers are​ built, the average cost per dulcimer can be estimated by ​C(x)equals0.1xsquaredminus0.3xplus2.025​, where​ C(x) is in hundreds of dollars. What is the minimum average cost per dulcimer and how many dulcimers should be built to achieve that​ minimum?

Answer 1

The minimum average cost per dulcimer is 1.8 hundred dollars,

1.5 hundred dulcimers should be built.

Step-by-step explanation:

Given function that represents the average cost ( in hundred of dollars ) per dulcimer,

`C(x)=0.1x^2-0.3x+2.025`

Differentiating with respect to x,

`C'(x) = 0.2x - 0.3`

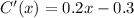
Again differentiating,

`C''(x) = 0.2`

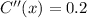
For maximum and minimum,

C'(x) = 0

0.2x - 0.3 = 0

0.2x = 0.3

`\implies x = (0.3)/(0.2)=1.5`

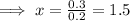
For x = 1.5,

C''(x) = positive,

Hence, C(x) is minimum for x = 1.5,

Minimum value = C(1.5) = 0.1(1.5)² - 0.3(1.5) + 2.025 = 0.1(2.25) - 0.45 + 2.025 = 1.8

Therefore, the minimum average cost per dulcimer is 1.8 hundred dollars for 1.5 hundred dulcimers.