Question

Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x+2, and BC = 3x+6, what is BC?

Answer 1

BC=30

Explanation:

AC = 48

AB = 2x+2

BC=3x+6

AC= AB + BC

48 = 2x+2+3x+6

48=5x+8

5x=40

x=8

Hence

BC = 3(8)+6

BC=24+6

BC=30

Answer 2

The value of BC is 30.

Explanation:

Given information: A, B, and C are collinear, B lies between A and C, AC = 48, AB = 2x+2, and BC = 3x+6.

If A, B, and C are collinear, B lies between A and C, then by using segment addition property, we get

`AB+BC=AC`

Substitute AC = 48, AB = 2x+2, and BC = 3x+6 in the above equation.

`(2x+2)+(3x+6)=48`

On combining like terms we get

`(2x+3x)+(2+6)=48`

`5x+8=48`

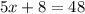
Subtract 8 from both sides.

`5x=48-8`

`5x=40`

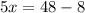
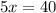
Divide 5 from both sides.

`x=8`

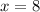
The value of x is 8.

We need to find the value of BC.

`BC=3x+6\Rightarrow 3(8)+6=30`

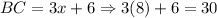
Therefore the value of BC is 30.