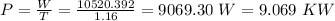Answer:
9.069 KW
Step-by-step explanation:
The heat engine operates in a carnot cycle between 75°C to 492°C so the lower temperature
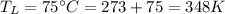 and the higher temperature
and the higher temperature
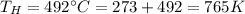
Efficiency of the carnot cycle
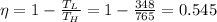
We know that
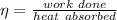
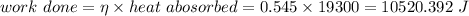
it is given that duration of each cycle is 1.16 sec so power output