Answer: (a) 0.002 (b)

Explanation:
Given : The probability that the IC in a radio came from one of the sources =
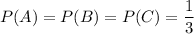
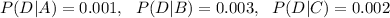
By using the law of total probability :-
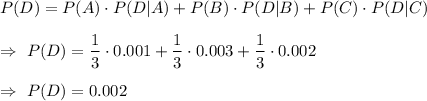
Hence, the probability that any given radio will contain a defective IC : 0.002
By using Bayes theorem , we have
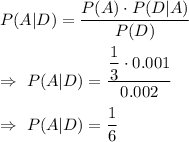
Hence, If a radio contains a defective IC, find the probability that it came from company A :
