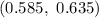Question

22.17) A 2015 Gallup survey asked respondents to consider several different foods and beverages and to indicate whether these were things that they actively tried to include in their diet, actively tried to avoid in their diet, or didn't think about at all. Of the 1009 adults surveyed, 616 indicated that they actively tried to avoid drinking regular soda or pop. Assume that the sample was an SRS. Based on the sample, the large-sample 90% confidence interval for the proportion of all American adults who actively try to avoid drinking regular soda or pop is...

Answer 1

Answer:
`(0.585,\ 0.635)`

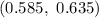
Explanation:

Given : The number of adults surveyed : n= 4009

The number of adults indicated that they actively tried to avoid drinking regular soda or pop.=616

The proportion of adults indicated that they actively tried to avoid drinking regular soda or pop=
`(616)/(1009)\approx0.61`

Significance level :
`\alpha=1-0.90=0.10`

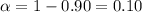
Critical value =
`z_(\alpha/2)=1.645`

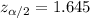
We assume that the sample is a simple random sample.

The confidence interval for population proportion is given by :-

`p\pm z_(\alpha/2)\sqrt{(p(1-p))/(n)}`

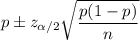
i.e.
`0.61\pm(1.645)\sqrt{(0.61(1-0.61))/(1009)}`

`\approx0.61\pm0.025=(0.61-0.025,\ 0.61+0.025)\\\\=(0.585,\ 0.635)`

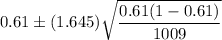
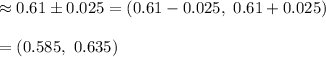
Hence, the 90% confidence interval for the proportion of all American adults who actively try to avoid drinking regular soda or pop is
`(0.585,\ 0.635)`