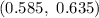Answer:
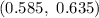
Explanation:
Given : The number of adults surveyed : n= 4009
The number of adults indicated that they actively tried to avoid drinking regular soda or pop.=616
The proportion of adults indicated that they actively tried to avoid drinking regular soda or pop=
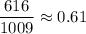
Significance level :
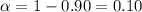
Critical value =
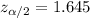
We assume that the sample is a simple random sample.
The confidence interval for population proportion is given by :-
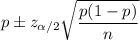
i.e.
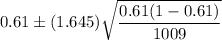
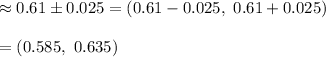
Hence, the 90% confidence interval for the proportion of all American adults who actively try to avoid drinking regular soda or pop is