Answer: First Option

Explanation:
We know that the mean is:

We know that the standard deviation is:
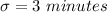
The formula to calculate the Z-scores is:
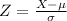
Where in this case
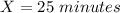
Then the z-score for
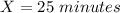 is:
is:
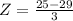
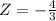
The negative number means that the deviation is to the left of the mean. In other words 25minutes is at 1.33 standard deviations to the left of the mean
