Question

. Consider a hypothetical reaction 2A + B → 3C, with a rate that is second order with respect to B and zero order with respect to A. How would doubling the concentration of A and increasing the concentration of B by a factor of three affect the rate of this reaction?

Answer 1

Answer: The final rate will become 9 times of the initial rate.

Explanation: Rate law says that rate of a reaction is directly proportional to the concentration of the reactants each raised to a stoichiometric coefficient determined experimentally called as order.

`Rate=k[A]^x[B]^y`

k= rate constant

x = order with respect to A

y = order with respect to B

n = x+y = Total order

`2A+B\rightarrow B+3C`

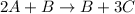
Rate law :
`Rate=k[A]^0[B]^2`, order with respect to A is 0, order with respect to B is 2 and total order is 2.

Given: doubling the concentration of A and increasing the concentration of B by a factor of three.

`Rate'=[tex]k[2A]^0[3B]^2`

`Rate'=k[2]^0[A]^0[3]^2[B]^2`

`Rate'=k* 1* [A]^0* 9* [B]^2`

`Rate'=Rate* 9`

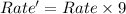
Thus the final rate will become 9 times of the initial rate.