Answer:
The domain of the function is:
x ≥ -4, x ≠ -2, x ≠ 5
Explanation:
Domain of a function--
A domain of a function is the set of all the input values i.e. the x-values for which a function is defined.
Here we are given a function f(x) as follows:

Now, we know that the domain of the function depends on the denominator as well as domain of the square root function.
Since, a rational function is defined at the points excluding the zero of the denominator function.
i.e.
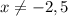
Also, a square root function is defined for all the non-negative values of the function inside the radical sign.
i.e.
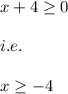
Hence, the domain is:
x ≥ -4, x ≠ -2, x ≠ 5