Question

Tell whether the set of ordered pairs satisfies an exponential function. Explain your answer.

{(-1, -5), (0, -3), (1, -1), (2, 1)}


Yes, because as the x-values are increasing by a constant amount, the y-values are being multiplied by a constant amount.


No, because as the x-values are increasing by a constant amount, the y-values are not being multiplied by a constant amount.

PLEASE ANSWER FASTTTTTT

Answer 1

Answer: Second Option

No, because as the x-values are increasing by a constant amount, the y-values are not being multiplied by a constant amount.

Explanation:

We have a set of ordered pairs of the form (x, y)

If a function is exponential then the ratio between the consecutive values of y, is always equal to a constant.

This means that:

`(y_2)/(y_1)=(y_3)/(y_2)=(y_4)/(y_3)=b`

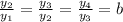
This is:
`y_2=by_1`

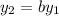
Now we have this set of points {(-1, -5), (0, -3), (1, -1), (2, 1)}

Observe that:

`(y_2)/(y_1)=(-3)/(-5)=(3)/(5)\\\\(y_3)/(y_2)=(-1)/(-3)=(1)/(3)\\\\(3)/(5)\\eq (1)/(3)`

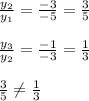
Then the values of y are not multiplied by a constant amount "b"

The function is not exponential