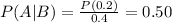Question

A group of 10 students participate in chess club, karate club, or neither.

Answer 1

Answer: Option B

`P(A|B)=0.50`

Explanation:

We look for the conditional probability of A given B.

This is written as:

`P(A|B) = (P(A\ and\ B))/(P(B))`

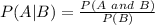
First we must find the probability of A and B

There are 10 students in total. Note that of those 10 students only 2 of them are at the same time in the karate club and in the chess club

Therefore:

`P(A\ and\ B)=(2)/(10)`

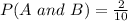
There are 10 students in total. Note that of those 10 students only 4 of them are in the chess club

Then:

`P(B)=(4)/(10)`

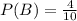
Finally:

`P(A|B) = (P(0.2))/(0.4)=0.50`