Question

TRUE OR FALSE: In single-slit diffraction, the central band gets thinner as the width of the slit increases.

Answer 1

Step-by-step explanation:

True

Answer 2

TRUE

Step-by-step explanation:

As we know that position of minimum intensity on the screen at a given angle of the screen is given by equation

`a sin\theta = N\lambda`

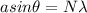
now for width of central maximum we will find the angular width of first minimum

`\beta = (2\lambda)/(a)`

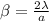
now linear width of the central bright fringe is given as

`w = L \beta`

`w = (2\lambda L)/(a)`

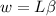
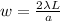
so we can say that if width of the central fringe will decrease by increasing the width of the slit as they as inversely dependent on each other

So its TRUE