Question

Maggie puts together two isosceles triangles so that they share a base, creating a kite. Each leg of the upper triangle measures 41 inches and each leg of the lower one measures 50 inches. If the length of the base of both triangles measures 80 inches, what is the length of the kite’s shorter diagonal?

Answer 1

The answer is 39 on edge. :)

Explanation:

Answer 2

Length of the kite’s shorter diagonal = 39.03 inches

Explanation:

Refer the given figure, we need to find DB,

Consider ΔABC,

Using cosine rule

`cos B=(a^2+c^2-b^2)/(2ac)`

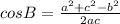
a = c = 41 inches

b = 80 inches

We need to find ∠B

Substituting

`cos B=(41^2+41^2-80^2)/(2* 41* 41)=-0.903\\\\B=154.56^0`

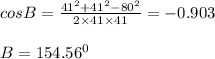
We can see that BD divides ∠B equally,

So,
`\angle ABD=(\angle B)/(2)=(154.56)/(2)=77.28^0`

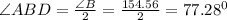
Now consider ΔABD,

Using sine rule

`(AB)/(sinD)=(AD)/(sinB)=(DB)/(sinA)`

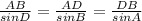
AB = 41 inches, AD = 50 inches, ∠B = 77.28°

Substituting

`(41)/(sinD)=(50)/(sin77.28)=(DB)/(sinA)\\\\sinD=0.7999\\\\D=53.12^0\\\\A=180-53.12-77.28=49.6^0\\\\(50)/(sin77.28)=(DB)/(sin49.6)\\\\DB=39.03inch`

Length of the kite’s shorter diagonal = 39.03 inches