Answer:
Length of the kite’s shorter diagonal = 39.03 inches
Explanation:
Refer the given figure, we need to find DB,
Consider ΔABC,
Using cosine rule
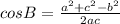
a = c = 41 inches
b = 80 inches
We need to find ∠B
Substituting
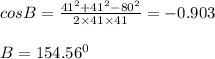
We can see that BD divides ∠B equally,
So,
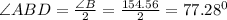
Now consider ΔABD,
Using sine rule
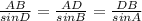
AB = 41 inches, AD = 50 inches, ∠B = 77.28°
Substituting

Length of the kite’s shorter diagonal = 39.03 inches