Answer:
Zeros:
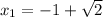
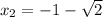
Interception with y-axis
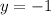
Vertex:
(-1, -2)
Explanation:
We have the following quadratic function
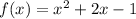
To find the zeros of the function, make
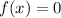 and solve for the variable x
and solve for the variable x
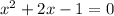
We must factor the expression. Then we use the quadratic formula:
For a function of the form
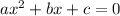 the quadratic formula is:
the quadratic formula is:
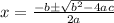
In this case note that:
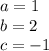
Then:

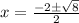
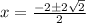
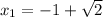
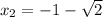
We know that the vertex of a quadratic function is at the point:
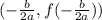
Then:

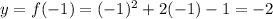
The vertex is: (-1, -2)
The intersection with the y-axis we find it doing
 and solving for y
and solving for y

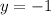
Look at the attached image.