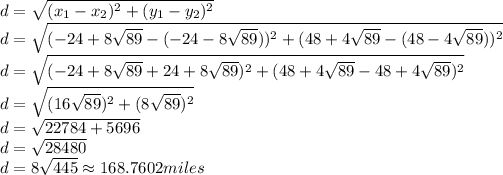Answer:
168.7602 miles
Explanation:
One way to solve this problem is by using an equation that describes the listening radius of the station, and another for the road, then the points where this two-equation intersect each other will represent when the driver starts and stops listening to the station, and the distance between the points is the miles that the driver will receive the signal.
The equation for the listening radius (the radio station is at (0,0)):

The equation for the road that past through the points (-120,0) and (80,100) (Collinsville and Harmony respectively):

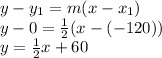
Substitutes the value of y in the equation of the circle:
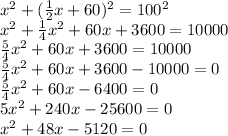
The formula to solve second-degree equations:

Using the values in x to find the values in y:
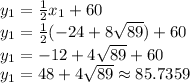

The distance between the points (51.4718,85.7359) and (-99.4718,10.2641) :