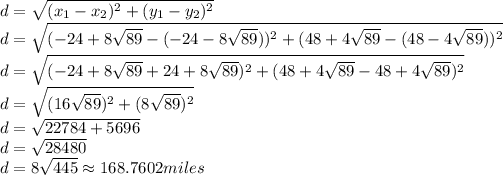Question

answer A radio station located 120 miles due east of Collinsville has a listening radius of 100 miles. A straight road joins Collinsville with Harmony, a town 200 miles to the east and 100 miles north. See the illustration. Suppose a driver leaves Collinsville and heads toward Harmony. For how many miles will the driver receive the signal?

Answer 1

168.7602 miles

Explanation:

One way to solve this problem is by using an equation that describes the listening radius of the station, and another for the road, then the points where this two-equation intersect each other will represent when the driver starts and stops listening to the station, and the distance between the points is the miles that the driver will receive the signal.

The equation for the listening radius (the radio station is at (0,0)):

`x^2+y^2=100^2`

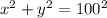
The equation for the road that past through the points (-120,0) and (80,100) (Collinsville and Harmony respectively):

`m=(y_2-y_1)/(x_2-x_1) =(100-0)/(80-(-120))=(100)/(200)=(1)/(2)`

`y-y_1=m(x-x_1)\\y-0=(1)/(2)(x-(-120))\\ y=(1)/(2)x+60`

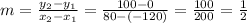
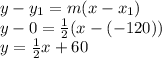
Substitutes the value of y in the equation of the circle:

`x^2+((1)/(2)x+60)^2=100^2\\x^2+(1)/(4) x^2+60x+3600=10000\\(5)/(4) x^2+60x+3600=10000\\(5)/(4) x^2+60x+3600-10000=0\\(5)/(4) x^2+60x-6400=0\\5 x^2+240x-25600=0\\x^2+48x-5120=0\\`

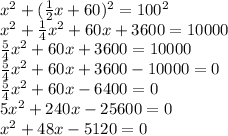
The formula to solve second-degree equations:

`x_(1,2)=(-b\pm√(b^2-4ac) )/(2a) \\x_(1,2)=(-48\pm√(48^2-4(1)(-5120)) )/(2(1))\\x_(1,2)=(-48\pm√(2304+20480) )/(2)\\x_(1,2)=(-48\pm√(22784) )/(2)\\x_(1,2)=(-48\pm16√(89) )/(2)\\x_(1,2)=-24\pm8√(89) \\x_1=-24+8√(89)\approx51.4718\\x_2=-24-8√(89)\approx-99.4718\\`

Using the values in x to find the values in y:

`y_1=(1)/(2)x_1+60\\y_1=(1)/(2)(-24+8√(89) )+60\\y_1=-12+4√(89)+60\\ y_1=48+4√(89)\approx85.7359`

`y_2=(1)/(2)x_2+60\\y_2=(1)/(2)(-24-8√(89) )+60\\y_1=-12-4√(89)+60\\ y_1=48-4√(89)\approx10.2641`

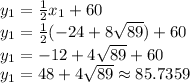
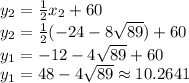
The distance between the points (51.4718,85.7359) and (-99.4718,10.2641) :

`d=√((x_1 -x_2 )^2+(y_1 -y_2)^2) \\d=\sqrt{(-24+8√(89) -(-24-8√(89)) )^2+(48+4√(89) -(48-4√(89)) )^2}\\d=\sqrt{(-24+8√(89) +24+8√(89) )^2+(48+4√(89) -48+4√(89) )^2}\\d=\sqrt{(16√(89) )^2+(8√(89) )^2}\\d=√(22784+5696)\\d=√(28480)\\d=8√(445)\approx168.7602miles`