Question

Perimeter the coordinates of the vertices of a quadrilateral are R(-1,3), S(3,3), T(5,-1), and U(-2,-1)

Answer 1

The perimeter is equal to
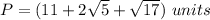`P=(11+2√(5)+√(17))\ units` or
`P=19.59\ units`

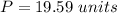
Explanation:

we have

The coordinates of the vertices are

R(-1,3), S(3,3), T(5,-1), and U(-2,-1)

plot the figure to better understand the problem

see the attached figure

we know that

The perimeter of a quadrilateral is the sum of its four length sides

so

`P=RS+ST+TU+UR`

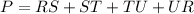
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

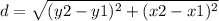
step 1

Find the distance RS

`R(-1,3)\\S(3,3)`

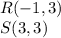
substitute the values

`d=\sqrt{(3-3)^(2)+(3+1)^(2)}`

`d=\sqrt{(0)^(2)+(4)^(2)}`

`RS=4\ units`

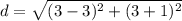
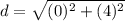
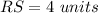
step 2

Find the distance ST

`S(3,3)\\T(5,-1)`

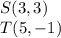
substitute the values

`d=\sqrt{(-1-3)^(2)+(5-3)^(2)}`

`d=\sqrt{(-4)^(2)+(2)^(2)}`

`ST=2√(5)\ units`

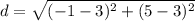
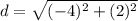
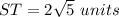
step 3

Find the distance TU

`T(5,-1)\\U(-2,-1)`

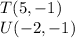
substitute the values

`d=\sqrt{(-1+1)^(2)+(-2-5)^(2)}`

`d=\sqrt{(0)^(2)+(-7)^(2)}`

`TU=7\ units`

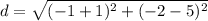
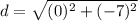
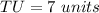
step 4

Find the distance UR

`U(-2,-1)\\R(-1,3)`

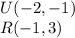
substitute the values

`d=\sqrt{(3+1)^(2)+(-1+2)^(2)}`

`d=\sqrt{(4)^(2)+(1)^(2)}`

`UR=√(17)\ units`

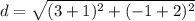
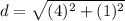
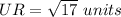
step 5

Find the perimeter

`P=RS+ST+TU+UR`

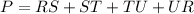
substitute the values

`P=4+2√(5)+7+√(17)`

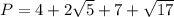
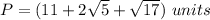`P=(11+2√(5)+√(17))\ units` -----> exact value

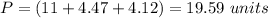`P=(11+4.47+4.12)=19.59\ units` -----> approximate value