Question

A thin, very light wire is wrapped around a drum that is free to rotate. The free end of the wire is attached to a ball of mass m. The drum has the same mass m. Its radius is R and its moment of inertia is I = (1/2)mR2 . As the ball falls, the drum spins. At an instant that the ball has translational kinetic energy K, what is the rotational kinetic energy of the drum?

Answer 1

`K_r = (K)/(2)`

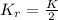
so kinetic energy of the drum is half the kinetic energy of the particle

Step-by-step explanation:

Here we know that the particle is connected with the drum through a string

So here we can say that velocity of the particle is same as the tangential velocity of the drum as the particle is connected with the string which is wounded on the drum

So here we can say

`v = r\omega`

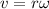
now kinetic energy of the particle is given as

`K = (1)/(2)mv^2`

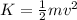
at the same time the rotational kinetic energy of the drum is given as

`K_r = (1)/(2)I\omega^2`

`K_r = (1)/(2)((1)/(2)mR^2)((v^2)/(R^2))`

`K_r = (1)/(4)mv^2`

`K_r = (K)/(2)`

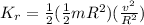
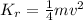
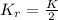
so kinetic energy of the drum is half the kinetic energy of the particle