Answer:
Activation energy of the reaction is 79.5 kJ/mol
Step-by-step explanation:
According to Arrhenius equation for a reaction-
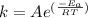
where k is the rate constant, A is the Arrhenius constant,
 is the activation energy and T is temperature in kelvin
is the activation energy and T is temperature in kelvin
For the given two different set of condition, we can write-
at
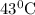 ,
,
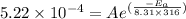 ............(1)
............(1)
at
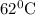 ,
,
 ............(2)
............(2)
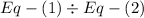 gives-
gives-
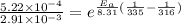
Solving this equation we get
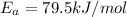
So activation energy of the reaction is 79.5 kJ/mol