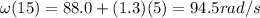(a) 88.0 rad/s
The angular speed of the wheel is

Keeping in mind that
1 revolution =
 radians
radians
The angular speed in radians/second can be found by solving the proportion:
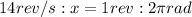
From which we find
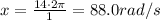
(b) 440 radians
Assuming the wheel is rotating at constant angular speed, the angular displacement of the wheel at time t is given by

where
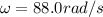 is the angular speed
is the angular speed
t is the time
Substituting
t = 5 s
we find the angle through which the wheel has rotated after 5 seconds:
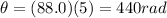
(c) 94.5 rad/s
The angular speed after a time t is given by
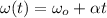
where
 is the angular speed at t=10 s, when the acceleration starts
is the angular speed at t=10 s, when the acceleration starts
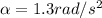 is the angular acceleration
is the angular acceleration
The duration of the acceleration is
t = 15 s - 10 s = 5 s
So substituting this value into the equation, we find the new angular speed: