Question

For some metal alloy it is known that the kinetics of recrystallization obey the Avrami equation, and that the value of k in the exponential is 2.60 x 10-6, for time in seconds. If, at some temperature, the rate of recrystallization is 0.0013 s-1, what total time (in s) is required for the recrystallization reaction to go to 90% completion?

Answer 1

t = 1456.8 sec

Step-by-step explanation:

given data:

contant k = 2.60*10^{-6}

rate of crystallization is 0.0013 s-1

rate of transformation is given by

`r = (1)/(t_0.5)`

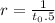
use specifies value to solve
`t_0.5`

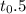
it is ime required for 50% tranformation

`r = (1)/(.0013)=769.2 sec`

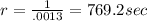
Avrami equation is given by

`y = 1 - e^(-kt^n)`

`0.5 = 1 - e^(-kt_0.5^n)`

`1-0.5 = e^(-kt_0.5^n)`

`ln (1 - 0.5) = -kt_0.5^n`

`ln (ln (1 - 0.5))/(-k) = nln t_0.5`

`n = ( ln (ln (1 - 0.5))/(-k))/(ln t_0.5)`

`n = ( ln (ln (1 - 0.5))/(-2.60*10^(-6)))/(ln 769.2)`

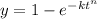
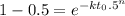
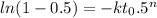
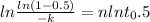
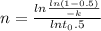
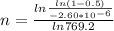
n = 1.88

second degree of recrystalization may be determine by rearranging original avrami equation

`t = [(-ln(1-y))/(k)]^(1/n)`

for 90%completion

`t = [(-ln(1-0.9))/(2.60*10^(-6))]^(1/1.88)`

t = 1456.8 sec