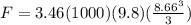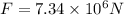Answer:
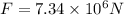
Step-by-step explanation:
Since each side of the triangular end is of equilateral triangle with side length a = 10 m
so height of the triangle h = a sin60
h = 10sin60 = 8.66 m
now we will take a small strip of width L and thickness dy at a depth of y from top
so here width L is given as
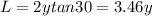
now the force on this small strip is given as
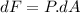
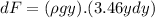
now the total force on the triangular part
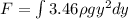
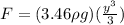
now the limits of y is from y = 0 to y = 8.66 m
so we have