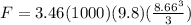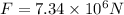Question

A trough is filled with a liquid of density 865 kg/m3. The ends of the trough are equilateral triangles with sides 10 m long and vertex at the bottom. Find the hydrostatic force on one end of the trough. (Use 9.8 m/s2 for the acceleration due to gravity.)

Answer 1

The hydrostatic force on one end of the trough is approximately 1835324.34 N.

Step-by-step explanation:

Calculate the area of the equilateral triangle end using its side length and the formula for triangle area.

Consider the pressure at the centroid of the triangle, which is equivalent to the average pressure acting on the entire surface. This pressure is calculated using the liquid's density, depth (half the triangle's height), and gravity.

Multiply the pressure obtained in step 2 by the area of the triangle from step 1 to get the total hydrostatic force acting on one end of the trough.

Answer 2

`F = 7.34 * 10^6 N`

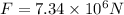
Step-by-step explanation:

Since each side of the triangular end is of equilateral triangle with side length a = 10 m

so height of the triangle h = a sin60

h = 10sin60 = 8.66 m

now we will take a small strip of width L and thickness dy at a depth of y from top

so here width L is given as

`L = 2ytan30 = 3.46 y`

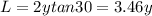
now the force on this small strip is given as

`dF = P . dA`

`dF = (\rho g y). (3.46 y dy)`

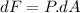
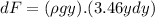
now the total force on the triangular part

`F = \int 3.46 \rho g y^2 dy`

`F = (3.46 \rho g)((y^3)/(3))`

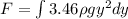
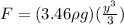
now the limits of y is from y = 0 to y = 8.66 m

so we have

`F = 3.46(1000)(9.8)((8.66^3)/(3))`

`F = 7.34 * 10^6 N`