Question

A triangle has A, B, and C located at(-3, 0). (3, 0), and (0, 4), respectively, on the coordinate plane. The medians of (triangle)ABC intersect

at the point with which coordinates? Round each coordinate to the nearest tenth if necessary.

A. (1.5, 2)

B. (-1.5, 2)

C. (0, 1.3)

D. (0, 0)

Answer 1

Given:

Vertices of a triangle ABC are A(-3,0), B(3,0) and C(0,4).

To find:

The intersection point of all the medians of the triangle ABC.

Solution:

We know that, intersection point of all the medians of a triangle is called centroid.

The formula of centroid is

`Centroid=\left((x_1+x_2+x_3)/(3),(y_1+y_2+y_3)/(3)\right)`

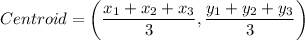
Vertices of a triangle ABC are A(-3,0), B(3,0) and C(0,4).

`Centroid=\left((-3+3+0)/(3),(0+0+4)/(3)\right)`

`Centroid=\left((0)/(3),(4)/(3)\right)`

`Centroid=\left(0,1.333...\right)`

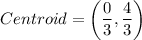
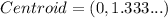
Round each coordinate to the nearest tenth.

`Centroid=\left(0,1.3\right)`

The coordinates of required point are (0,1.3). Therefore, the correct option is C.