Given:
Vertices of a triangle ABC are A(-3,0), B(3,0) and C(0,4).
To find:
The intersection point of all the medians of the triangle ABC.
Solution:
We know that, intersection point of all the medians of a triangle is called centroid.
The formula of centroid is
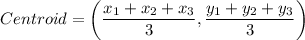
Vertices of a triangle ABC are A(-3,0), B(3,0) and C(0,4).
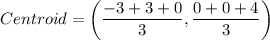
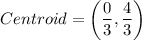
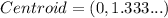
Round each coordinate to the nearest tenth.
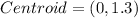
The coordinates of required point are (0,1.3). Therefore, the correct option is C.