Question

We are interested in the dimensions of a certain square a rectangle had length triple the side of this square and width two units less than the side of this square. If the two areas are equal, what are the squares dimensions (W x H)

Answer 1

Let s be the side length of the square. The dimensions of the rectangle are three times the side of the square (i.e. 3s), and two less than the side of the square (i.e. s-2).

So, the area of this rectangle is

`3s(s-2)=3s^2-6s`

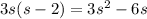
The area of the square is
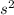`s^2`, and we know that the two areas are the same, so we have

`3s^2-6s=s^2 \iff 2s^2-6s=0 \iff 2s(s-3)=0 \iff s=0 \lor s=3`

The solution s=0 would lead to the extreme case where the rectangle and the square are actually a point, so we accept the solution s=3.