Question

The carbon-carbon (C―C) bond has an average bond energy of 347 kJ/mol, which is the energy required to break one mole of C―C bonds. What is the wavelength of the photon that can break this bond? 487 nm 457 nm 354 nm 345 nm 377 nm

(1) 457 nm
(2) 487 nm
(3) 345 nm
(4) 354 nm
(5) 377 nm

Answer 1

(3) 345 nm

Step-by-step explanation:

Given:

Average C-C bond energy = 347 kJ/mol

To determine:

Wavelength of photon that can break a C-C bond

Calculation:

The energy (E) of a photon is related to its wavelength (λ) by the Planck's equation:

`E = (hc)/(\lambda )`

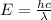
where h = Planck's constant = 6.626*10⁻³⁴ Js

c = speed of light = 3*10⁸ m/s

`\lambda = (hc)/(E)`

`\lambda =(6.626*10^(-34)Js*3*10^(8)ms^(-1)*6.023*10^(23)mol^(-1))/(347,000Jmol^(-1))`

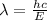
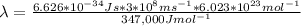
λ = 3.45*10⁻⁷ m

Since 1 nanometer (nm) = 10⁻⁹ m

The calculated wavelength corresponds to 345 nm