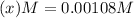Answer : The concentration of
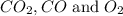 at equilibrium will be, 0.598 M, 0.00216 M and 0.00108 M respectively.
at equilibrium will be, 0.598 M, 0.00216 M and 0.00108 M respectively.
Explanation : Given,
Equilibrium constant =
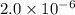
tex]\text{Concentration of }CO_2=\frac{\text{Moles of }CO_2}{\text{Volume of solution}}=\frac{3.0mole}{5.0L}=0.6mole=0.6M[/tex]
The balanced equilibrium reaction is,
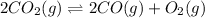
Initial conc. 0.6 M 0 0
At eqm. (0.6-2x) M 2x M x M
The expression of equilibrium constant for the reaction will be:
![K_c=([CO]^2[O_2])/([CO_2]^2)](https://img.qammunity.org/2020/formulas/chemistry/college/kziv6pqk53v4iv58sjkjzp92nbbt3brx0t.png)
Now put all the values in this expression, we get :
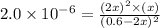
By solving the term 'x', we get:
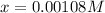
Concentration of
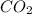 at equilibrium =
at equilibrium =
![(0.6-2x)M=[0.6-2(0.00108)]M=0.598M](https://img.qammunity.org/2020/formulas/chemistry/college/1m3d8cfwoh0qae4tavhbsvkiu02788i6r6.png)
Concentration of
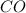 at equilibrium =
at equilibrium =
![(2x)M=[2(0.00108)]M=0.00216M](https://img.qammunity.org/2020/formulas/chemistry/college/g43d87huvu0jfl0f0fcf7n1xqgifbimcbl.png)
Concentration of
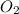 at equilibrium =
at equilibrium =