Answer:
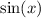 is an odd function.
is an odd function.
Explanation:
We are asked to prove whether
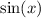 is even or odd.
is even or odd.
We know that a function
 is even if
is even if
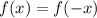 and a function
and a function
 is odd, when
is odd, when
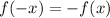 .
.
We also know that an even function is symmetric with respect to y-axis and an odd function is symmetric about the origin.
Upon looking at our attachment, we can see that
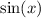 is symmetric with respect to origin, therefore,
is symmetric with respect to origin, therefore,
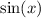 is an odd function.
is an odd function.