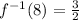Question

If f(x) and f-1(x) are inverse functions of each other and f(x)=2x+5,what isf-1(8)?

Answer 1

`f ^(-1) (8) = (3)/(2)`

Explanation:

We know the function
`f(x)`

`f (x) = 2x +5`

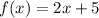
We want to find

`f ^(-1) (8)`

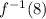
Remember that if we have a function
`f(x)` and its inverse
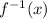`f ^ {-1}(x)`, then the domain of the function
`f^(-1)(x)` will be the range of the function
`f(x)`.

This means that to find
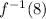`f ^ {-1}(8)` we must look for:

`f (x) = 2x +5 = 8`

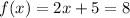
We solve the equation for x.

`2x + 5 = 8\\\\2x = 8-5\\\\2x = 3\\\\x = (3)/(2)`

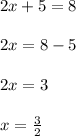
So:

`f ^(-1) (8) = (3)/(2)`