Question

Recall that N = {1,2,3….}. Let f: N -> N be defined by f(x) = x+1. Give a counterexample to the claim that f is onto.

Also, Let G: R -> R be defined by g(x)=x2. Give a counterexample to the claim that g is one to one.

Answer 1

Answer: The examples are given below.

Step-by-step explanation: Given that N = {1, 2, 3, . . .}. A function f : N --> N is defined by

f(x) = x + 1.

We are to give a counterexample to the claim that f is onto.

Let us consider the element 1 in he co domain N such that

`f(x)=1\\\\\Rightarrow x+1=1\\\\\Rightarrow x=1-1\\\\\Rightarrow x=0`

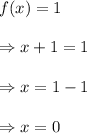
Since 0 does not belong to N, so there exists an element in the domain whose image does not exist in the co domain.

Therefore, the given function is NOT onto.

We are given another function g : R --> R defined by

g(x) = x².

We are to give a counterexample to the claim that g is one to one.

Let us consider the element 1 in the co domain R.

We see that

`f(x)=1\\\\\Rightarrow x^2=1\\\\\Rightarrow x=\pm1`

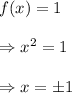
So, there exists two elements 1 and -1 in the domain having the same image 1 in the co domain.

Therefore, the function g(x) is not one to one.