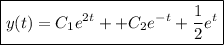Question

Find the general solution to the equation y" – y' – 2y=-et

Answer 1

`y''-y'-2y=-e^t`

The corresponding homogeneous ODE is

`y''-y'-2y=0`

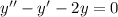
with characteristic equation

`r^2-r-2=(r-2)(r+1)=0`

with roots at
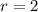`r=2` and
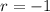`r=-1`, so the characteristic solution is

`y_c=C_1e^(2t)+C_2e^(-t)`

For the non-homogeneous ODE, assume a particular solution of the form

`y_p=ae^t`

`\implies{y_p}'=ae^t`

`\implies{y_p}''=ae^t`

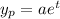
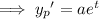
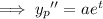
Substituting
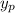`y_p` and its derivatives into the ODE gives

`ae^t-ae^t-2ae^t=-e^t`

`-2ae^t=-e^t`

`\implies-2a=-1\implies a=\frac12`

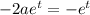
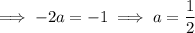
Then the ODE has the general solution

`\boxed{y(t)=C_1e^(2t)++C_2e^(-t)+\frac12e^t}`